نقد و بررسی تابع نمایی و لگاریتمی ( آموزش ۱۰۰٪ )

هدف ما از نوشتن نقد و بررسی تابع نمایی و لگاریتمی هموار کردن راه یادگیری برای دانش آموزان هست تا به امید خدا هیچ دانشآموزی به علت ضعف تدریس در یادگیری و عدم کسب مناسب علم دچار مشکل نشه.
از بچگی بهمون گفتن درس بخون تا دکتر بشی، امتحاناتت رو با نمره خوب قبول شو تا مهندس بشی! اما هیچکس به ما نگفت چجوری… ما خودمون میدونستیم که برای آیندۀ بهتر باید تلاش بیشتری داشته باشیم، اما خیلی وقتها آدمها برای تلاش کردن نیاز به مشوق و انگیزه دارن. برای قرار گرفتن توی مسیر صعود و پلههای ترقی نیاز به راهنمایی دارن.
همونطور که پیش از این گفتیم این مطلب برای هموار کردن راه دانش آموزان موردبررسی قرار گرفته شده. یکی از مسائلی که همیشه توی دوران دبیرستان و حتی دانشکدههای مهندسی مطرح بوده و هست، تابع نمایی و لگاریتمی بوده.
امروزه به دلیل شیوع و همهگیری ویروس کووید-19 بسیاری از آموزشها به تدریس مجازی روی آوردن و طی بازخورد یک سال گذشته این طرح تا حد زیادی موفق بوده و تونسته جانشین تدریس حضوری باشه. البته بالطبع مشکل والدین و دانش آموزان نحوه یادگیری و طریقه آموزشی نیست، چیزی که حائز اهمیته آینه که تدریس چه حضوری و چه غیر حضوری بازخورد کاملی رو ارائه بده.
توی همین راستا، «ریاضی رو خط» پکیجی شامل ویدئوها و جزوات مربوط به تابع نمایی و لگاریتمی آماده کرده تا خلأ مربوط به یادگیری در مورد عناوین مربوطه رو پر کنه.
از مزایای این پکیج عدم نیاز به خرید مستقیم اون هست، به صورتی که شما تنها با تهیه اشتراک میتونین دسترسی کاملی به پکیج آموزشی و یادگیری «اولین موسسه آموزشی و آنلاین ایران» داشته باشین.
شما با تهیه اشتراک به موارد بسیاری مثل، همه دورههای آموزشی، پشتیبانی ۲۴ ساعته و تضمین موفقیت توی کنکور دسترسی پیدا میکنین که با توجه به نقش پررنگ ریاضی توی کنکور این مورد برای شما میتونه خیلی پرکاربرد باشه.
البته جزوه و ویدئوهای آموزشی نمونه در ادامه با توضیح مختصر اما کاملی که درمورد توابع نمایی و لگاریتمی ارائه میشه رو برای شما قرار دادیم تا برتری پکیج آموزشیمون رو به اثبات برسونیم.
تعریف تابع نمایی
«تابع نمایی (exponential function)، در ریاضیات، رابطهای به شکل y = aˣ هست (a به توان x)، با متغیر مستقل x که در کل خط اعداد حقیقی بهعنوان توان یک عدد مثبت a قرار دارن. احتمالاً مهمترین توابع نمایی y = eˣ (e به توان x) هست که گاهی اوقات نوشته میشه y = exp (x)، توی این فرمول e به مقدار (2.7182818…) (round = 2.71) تعریف میشه.
البته پایه سیستم طبیعی لگاریتمها (ln) هست. طبق تعریف، x یک لگاریتمه و بنابراین یک تابع لگاریتمی وجود داره که معکوس تابع نمایی هست. به طور خاص، اگر y = eˣ (e به توان x)، پس x = ln y. تابع نمایی هم به عنوان مجموع سری بینهایت تعریف میشه.»
خواص تابع نمایی
جالبه بدونین که قوانین تابع نمایی درست مثل توان تو بحثهای محاسباتی هست.
مثلاً همونطور که اگر توی ضرب پایهها برابر و توانها متفاوت باشه، یک پایه رو مینویسیم و توانها رو جمع میکنیم، توی تابع نمایی e هم دقیقاً این خاصیت صدق میکنه:
eᵃ.eᵇ=eᵃ+ᵇ
یا:
ᵇ(eᵃ)=eᵃᵇ

نمودار تابع نمایی
اگر a به عنوان عدد پایه بزرگتر از صفر یا یک عدد نامنفی باشه (a>0)، نمودار تابع نمایی در جهت مثبت بی نهایت (∞+)، به صورت صعودی شناخته میشه؛ و در صورتی که a کوچیکتر از صفر و یا یک عدد منفی باشه (a<0)، نمودار تابع نمایی در جهت منفی بی نهایت (∞-)، یعنی در جهت نزولی حرکت میکنه.
به این ترتیب:
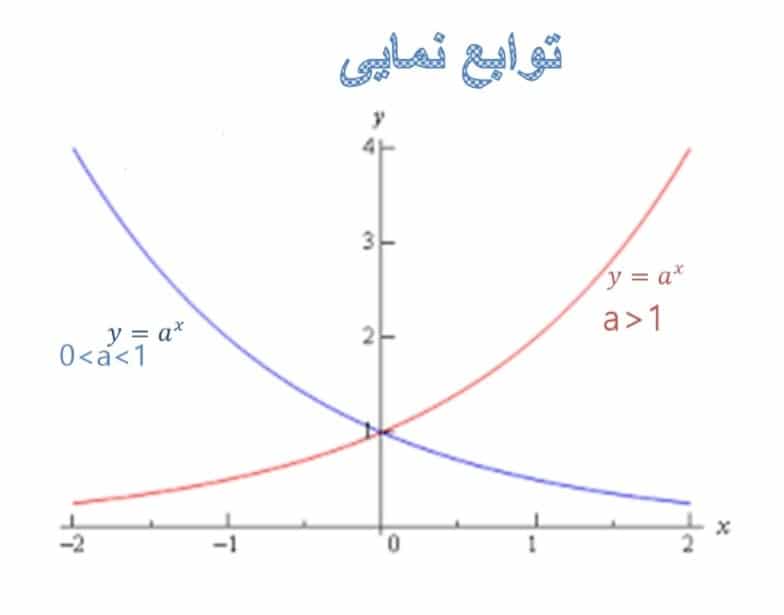
تعریف تابع لگاریتمی
در حقیقت توابع لگاریتمی معکوس توابع نمایی هستن و هر تابع نمایی رو میتونیم به صورت لگاریتمی هم بیان کنیم. به طور مشابه، تمام توابع لگاریتمی رو نیز میشه به صورت نمایی بازنویسی کرد. لگاریتمها واقعاً مفید هستن و به ما اجازه میدن با اعداد بسیار بزرگ کار کنیم و در عین حال اعدادی با اندازه بسیار قابل کنترل تر رو دستکاری کنیم.
اگر بخوایم همینطوری y x = 2 y حل کنیم تا بشه اون رو به شکل تابع نوشت، یک کلمه یا نماد جدید باید معرفی بشه. اگر x = 2 y ، اون وقت y = (پایه یا بر مبنای 2) برابر با x هست. کلمه لگاریتم، به اختصار ورود به سیستم، برای ارضای این نیاز معرفی شده.
y = (مبنای 2) برابر با x
این معادله به صورت y = log 2ˣ بازنویسی میشه و خونده میشه: لگاریتم ایکس بر مبنای دو.
این بحث به صورت «y برابر است با لگاریتم x، بر مبنای 2» یا «y برابر است با گزارش، مبنای 2، از x» هم تعریف میشه. البته میشه به جای کلمه مبنا از پایه هم استفاده کرد.
خواص و مشتق تابع لگاریتمی
گفتیم که تابع لگاریتمی همون معکوس تابع نمایی هست، پس طبیعیه که خواص و قوانین این دو تابع مشابه هم باشن، به طوری که توی محاسبات توابع لگاریتمی هم دقیقاً از همون فرآیندهای تابع نمایی پیروی میکنیم؛ اما تنها یک تفاوت وجود داره که بسیار ساده هست و واقعاً جای نگرانی وجود نداره.
مثالهای مشابه تابع نمایی:
ˡᵒᵍaᵘ+ˡᵒᵍaᵛ=ˡᵒᵍaᵘᵛ
در صورتی که مبنا یا پایهها برابر باشن اعداد ضریب رو مثل توان جمع میکنیم.
مثال متفاوت از تابع لگاریتمی، برای توان ضریب لگاریتم:
ˡᵒᵍauᵛ=ᵛˡᵒᵍaᵘ
توی توضیح مثالی که داده شده بود باید بگیم که توان خود لگاریتم یا ضریب لگاریتم به پشت لگاریتم منتقل میشه و مبنا و ضریب سر جای خودشون باقی میمونن.
به این ترتیب:

نمودار تابع لگاریتمی
معکوس توابع نمایی توابع لگاریتمی (logariyhm) هست که نمودار اون بر اساس اینکه متغیر پایه یعنی a بزرگتر از صفر و یک عدد نامنفی (a>0) باشه، به موازات محور x ها تعیین میشه. یعنی قرینه تابع نمایی نسبت به محور x:
استفاده از توابع لگاریتمی
کاربرد لگاریتمها مفید بودن اونها توی حل معادلات نمایی محسوب میشه. برخی از نمونههای اون عبارت هستن از صدا (معیارهای دسی بل)، زلزله (مقیاس ریشتر)، روشنایی ستارگان و شیمی (تعادل pH، معیار اسیدیته و قلیاییت).
خلاصه که لگاریتم واقعاً کاربرد گستردهای توی جهان اطراف ما و حل مباحث محاسباتی داره. همونطور که گفتیم لگاریتم و تابع نمایی تنها به دوران دبیرستان و کنکور ختم نمیشن و توی دانشگاه هم مورد استفاده قرار میگیرن، شما برای یادگیری توابع جبری، انتگرال، دیفرانسیل و خیلی مباحث دیگه به توابع نمایی و لگاریتم نیاز خواهید داشت. پس بهتره که توی همین دوره دبیرستان این مسائل رو خوب یاد بگیرین تا هم کنکور رو عالی بگذرونین و هم توی دانشکده ازشون استفاده کنین.
ریاضی رو خط با بهترین اساتید و پرکاربردترین متدها اینجاست تا خیال شما رو از بابت یادگیری تمامی مسائل ریاضی راحت کنه. فراموش نکنین که موفقیت شما اعتبار مجموعه ماست.
به ایسنتاگرام ما ببپیوندید

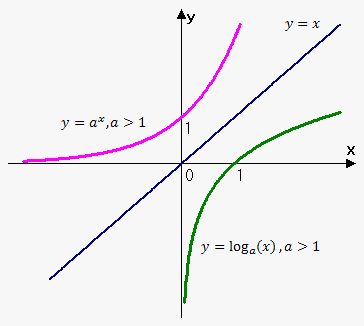






دیدگاهتان را بنویسید