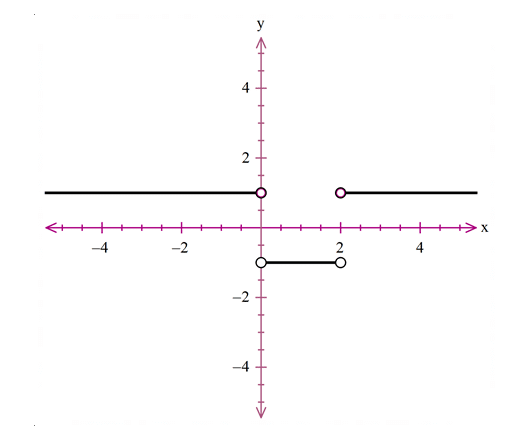
پکیج آموزشی قدرمطلق را در این مقاله بررسی می کنیم ، شما بعد از مطالع این مقاله دید کلی به قدر مطلق پیدا می کنید.

نمایش ریاضی قدرمطلق :

قدر مطلق | x = | x

مقدار x به صورت غیر منفی

قدرمطلق منفی ها را قرینه میکند تا آنهارا مثبت کند.
نماد |x| توسط وایراستراس (Karl Weierstrass) در سال 1841 پیشنهاد داده شد.

شما عزیزان میتوانید صفر تا صد مبحث قدرمطلق شامل:

(تعریف قدرمطلق ، خواص قدرمطلق ، معادلات و نامعادلات قدرمطلقی ، چند ضابطه ای کردن توابع قدرمطلقی به کمک تعیین علامت ، رسم توابع قدرمطلقی و …. را در پکیج قدرمطلق آموزش ببینید، این پکیج شامل ویدیو های آموزشی ، جزوات که بر اساس تمرین و تکرار تهیه شده اند و همچنین آزمون های طبقه بندی شده قرار گرفته شده است.(لینک)

هزار تومان ۱۲۵ ماهانه

دسترسی به همه دوره ها
پشتیبانی آنلاین 24 ساعته
تضمین موفقیت در آزمون ها و کنکور

تعبیر تابع قدر مطلق :

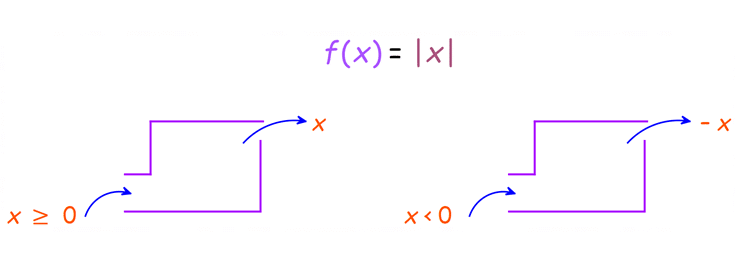
تعبیر تابع قدرمطلق به صورت یک ماشین که از منفی خوشش نمیاد ( به مثبت ها کاری نداره) و منفی هارا تبدیل به مثبت (قرینه) میکند.

تعبیر هندسی قدر مطلق

قدرمطلق هر عدد حقیقی برابر است با فاصلهء آن نقطه روی محور اعداد تا مبدا مختصات (تا صفر)

دقت کنید فاصلهء بین دو نقطه همیشه مثبت یا صفر است.

|a=|6 یعنی نقاطی که فاصله آنها تا مبدا برابر 6 است .

دقت کردید دو نقطه وجود دارد که فاصله آنها از مبدا برابر 6 است : -6 و 6

برای همینه که داریم :

و به همین دلیل جواب ندارد ، (فاصله منفی نمیشود)

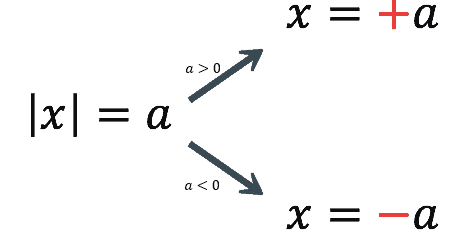
یک مثال ساده در رابطه با پکیج آموزشی قدرمطلق باهم حل کنیم :

مفهوم > |a>0 : |x روی محور اعداد

x| < a| : مجموعه نقاطی که فاصلهء آنها از مبدا کوچکتر یا مساوی a باشد.

تمام نقاط روی خط بالا خاصیت مورد نظر مارا دارند یعنی فاصله آنها تا مبدا کمتر از a است، یعنی :

x|<a ≡ -a<x<a|

به همین ترتیب |a>|x ; صفر از a کوچکتر مجموعه نقاطی است که فاصلهء آنها از مبدا بیشتر از a باشد . به نمودار زیر دقت کامل کنید.

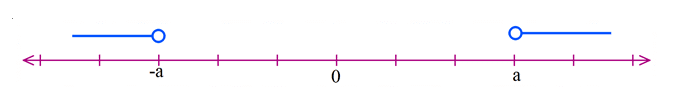
هر نقطه روی خطوط بالا را در نظر بگیرید و فاصلهء آن تا o (مبدا) را اندازه بگیریم از a بزرگتر است .

x|>a ⟹ x>a| یا x<-a

مثالی دیگر در رابطه با پکیج آموزشی قدرمطلق

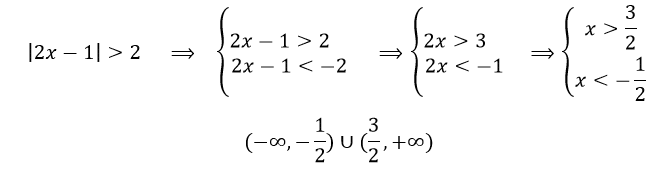
حل چند نامعدله قدرمطلقی :

هزار تومان ۱۲۵ ماهانه

دسترسی به همه دوره ها
پشتیبانی آنلاین 24 ساعته
تضمین موفقیت در آزمون ها و کنکور

رسم چند نمودار :

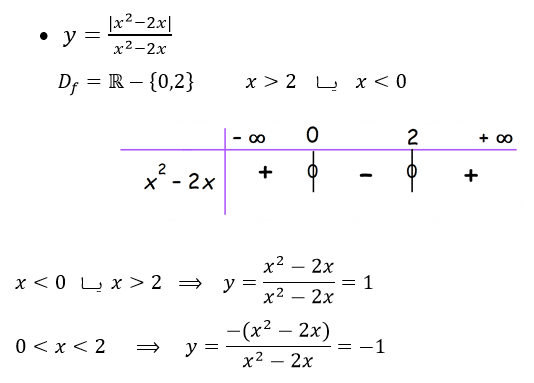
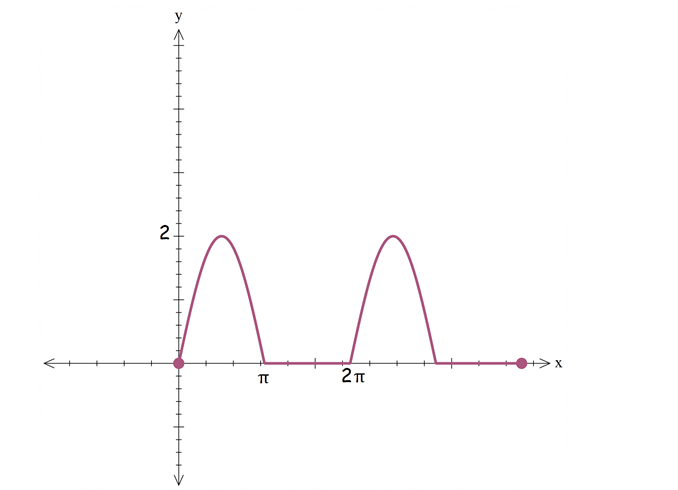
y=|sinx|+sinx 0≤x≤4π

0≤x≤π → y=sinx+sinx=2sinx

π≤x≤2π → y=-sinx+sinx=0

نکته مهم در رابطه با پکیج آموزشی قدر مطلق :

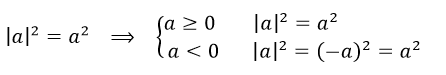
(a^2 )√=|a|

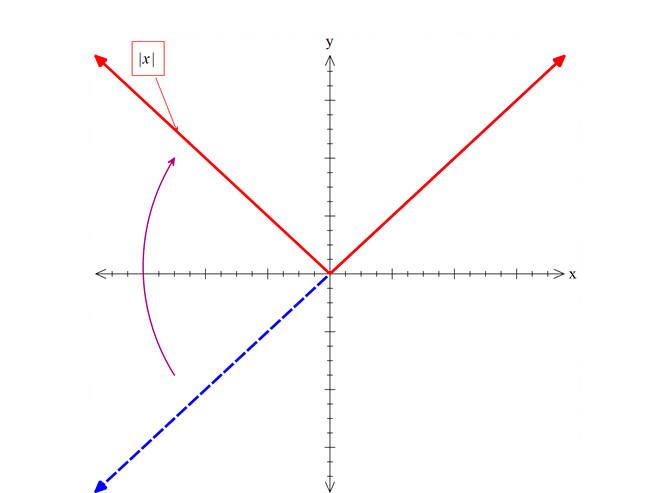
رسم نمودار |x| :

ابتدا y=x را رسم میکنیم ، |x| همواره نامنفی است بنابراین قسمت منفی (زیر محور x هارا ) خط میزنیم و قرینه آن را بالای محور رسم میکنیم.

رسم چند نمودار قدرمطلقی: (قواعد رسم وانتقال را در جزوه قدرمطلق ریاضی رو خط مطالعه نمایید)

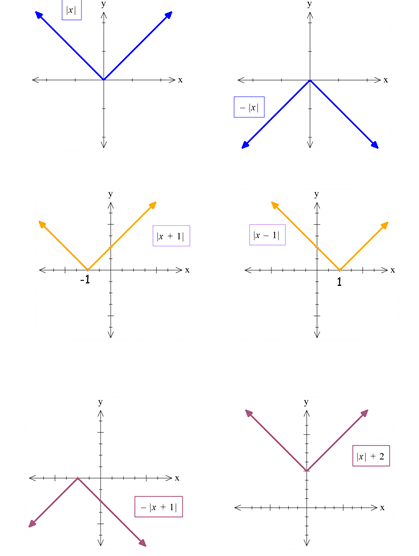
همه ی نمودار های بالا را میتوانیم به کمک استفاده از تابع |x| و قوانین انتقال رسم کنیم ، برای مطالعه این بخش مهم به پکیج قدرمطلق مراجعه نمایید.
استاد نوید خوانین زاده در پکیچ قدرمطلق ریاضی رو خط به طور جزیی و تخصصی به بیان مفهوم قدرمطلق پرداخته اند ، این پکیج شامل هر نوع سوال قدرمطلقی مانند : معادله و نامعادله قدرمطلقی، رسم نمودار و انتقال ، مساحت بین دو نمودار ، تعین علامت عبارت های قدرمطلقی و … میباشد .
به شما این اطمینان را میدهیم با آموزش از طریق این پکیج هیچ ابهامی در سوالات قدرمطلق نخواهید داشت

برای اطلاع از آخرین اخبار به اینستاگرام ما بپیوندید.