اهمیت علم آمار و آموزش آمار
ما در این مقاله به اهمیت و آموزش علم آمار, فرمول های محاسباتی , چارکها در علم آمار و تمامی فرمول های آن را بررسی کردیم. امیدپاریم برای شما مفید باشه.
علم آمار (statistics) را به عنوان دانشی تعریف میکنند که به مطالعه ، تحلیل و تفسیر ، ارائه و سازماندهی داده ها میپردازد.
در واقع علم آمار و آموزش آمار عمل استخراج و توسعهی دانشهای تجربی انسانی با استفاده از روش های گردآوری یا تنظیم ، پرورش و تحلیل است.
ما در عصر اطلاعات زندگی میکنیم و همواره در حال درک و دریافت داده های زیادی از دنیای اطرافمان هستیم که برای استفاده از این اطلاعات لازم است آنهارا به کمک آمار و به صورت ریاضی بیان کرده و استفاده کنیم.
آیا میدانید ریاضی رو خط جهت برقراری نظم آموزشی پای به میدان گذاشته و شرایطی بسیار عالی و آموزشی با کیفیت را برای دانش آموزان نهم تا کنکور فراهم کرده.
آمار شاخه ای از ریاضیات کاربردی است و به مجموعه ای از معادلات ریاضی گفته میشود که برای تجزیه و تحلیل آنچه در دنیای اطراف ما رخ میدهد مورد استفاده قرار میگیرد.
علم آمار در دو شاخهی آمار توصیفی و آمار استنباطی مورد بحث و بررسی قرار داده میشود.
داده های آماری به دو دسته تقسیم میشوند:
دادههای کمی : این دسته از داده ها از طریق شمارش یا سنجش با ابزارهای اندازهگیری بدست میآیند.
این نوع دادهها بوسیلهی اعداد نمایش داده میشوند.مانند طول ، وزن ، فشار ، دما …..
از آنجایی که این داده ها به صورت عددی هستند امکان انجام محاسبات ریاضی روی آنها وجود دارد .
دادههای کمی به دو دستهی کمی پیوسته و کمی گسسته تقسیم میشوند.
دادههای کیفی: این دادهها برعکس دادههای کمی از طریق شمارش بدست نمیآیند.
هم الان در سایت ریاضی رو خط عضو شوید
این نوع داده ها اغلب با صفت یا ویژگی در جامعهء آماری در رابطه هستند.
ویژگی هایی مانند : محل تولد ، گروه خونی ، مراحل رشد فردی و … از نوع کیفی هستند.
دادههای کیفی به دو دستهی کیفی ترتیبی و کیفی اسمی تقسیم میشوند.
ما تا اینجا با بخشی اهمیت علم آمار و آموزش آمار آشنا شدیم
محاسبه شاخصهای مرکزی برای دادههای کیفی و کمی:
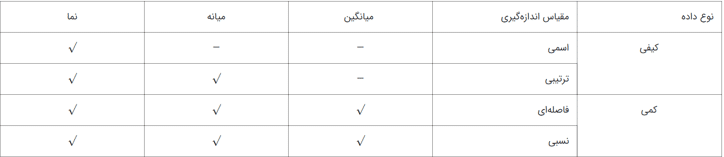
آمار توصیفی(Descriptive statistics)
تنظیم و طبقه بندی داده ها ، نمایش ترسیمی و محاسبه مقادیری از قبیل نما ، میانه و میانگین و … میباشد.
به طور کلی از سه روش در آمار توصیفی برای خلاصه سازی داده ها استفاده میشود:
- استفاده از جدول
- استفاده از نمودار
- محاسبه مقادیری خاص که نشان دهندهی خصوصیات مهمی از داده ها باشند.
روشهای خلاصه سازی داده ها در آمار توصیفی:
- تشکیل جدول توزیع فراوانی: توزیع فراوانی عبارت است سازمان دادن داده ها یا مشاهدات ، به صورت طبقات همراه با فراوانی هر طبقه .
تشکیل جدول فراوانی یک روش اقتصادی و در عین حال آسان برای نمایش انبوهی از داده های نامنظم است.
- ترسیم نمودار : یکی از نقاط ضعف نمایش داده ها به صورت جدول فراوانی عدم درک سریع اطلاعات جدول است .
نمودارها ابزارهای مناسبی برای نمایش تصویری اطلاعات هستند.
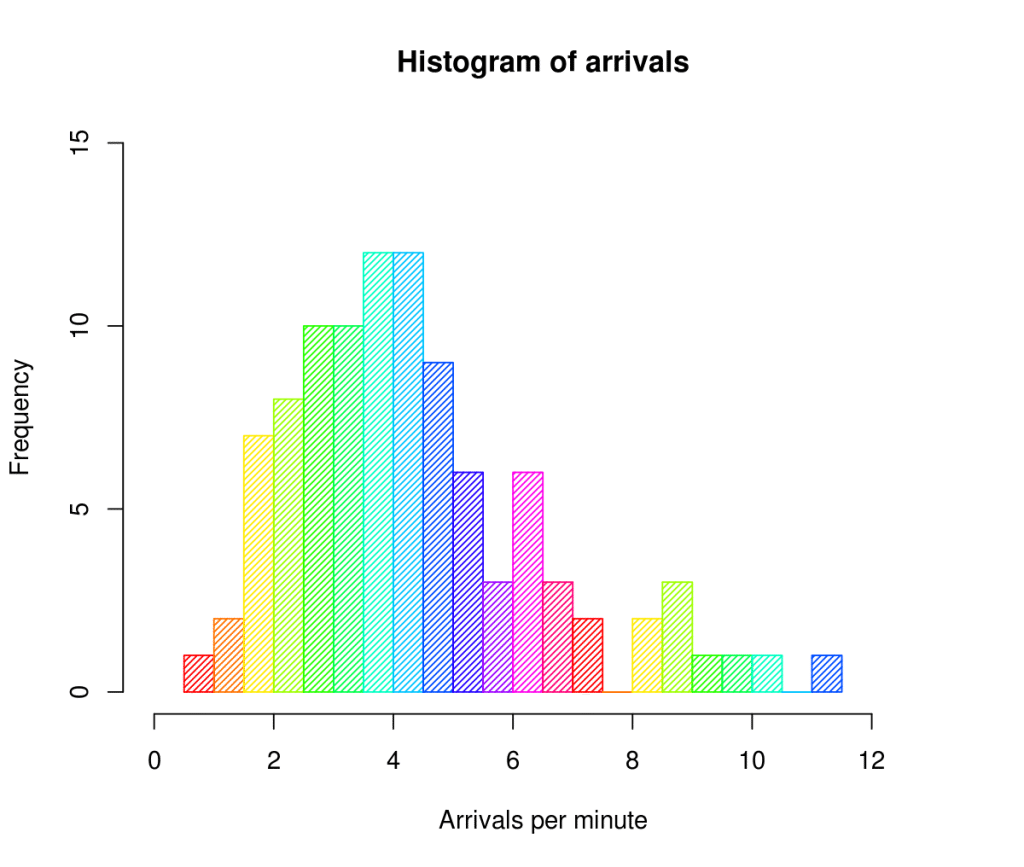
- نمودار بافت نگاشت ( Histogram) :
نمودار بافتنگار یا بافتنگاشت یا هیستوگرام نمایشی از توزیع دادههای کمی پیوستهاست که میتواند تخمینی ازتوزیع احتمال باشد.
نمودار ها بخشی بسیار بزرگی از علم آمار تشکیل می دهند
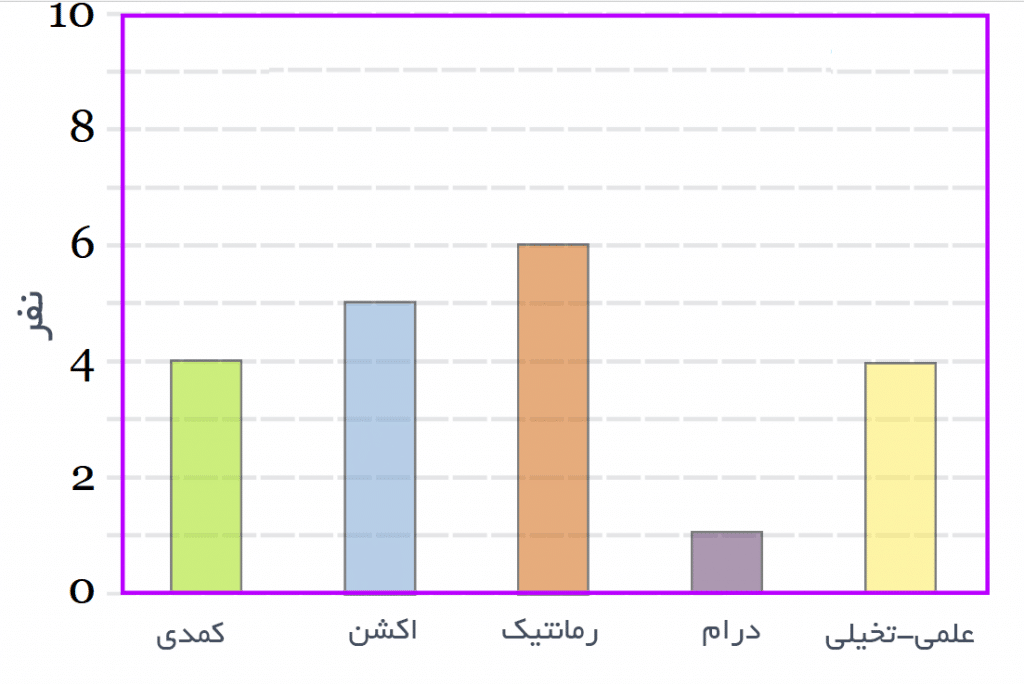
نمودار میلهای یا ستونی(Bar chart):
نمودار میلهای شامل مجموعه ای از ستون هاست که با فاصله یکنواختی در کنار هم قرار می گیرند و هر ستون مختصّ یک طبقه از متغیر و طول آن متناسب با فراوانی یا درصد آن طبقه است.
نمودار ستونی برای متغیرهای کیفی (اسمی و ترتیبی) به کار می رود، اما برای متغیر کمّی که تعداد طبقات آن کم باشد هم قابل استفاده است. به عنوان مثال چنانچه متغیری به نام تعداد فرزند داشته باشیم و در نمونه نهایی تعداد فرزندان هر خانواده از 1 تا 5 فرزند باشد و در واقع تعداد فرزندان شامل 5 طبقه باشد بازهم می توانیم از این نمودار استفاده کنیم. در مثال کتاب، می توان برای متغیرهای تحصیلات پدر، قومیت و درآمد اقدام به ترسیم نمودار ستونی نمود.
اگر سوالاتی در رابطه با اهمیت علم آمار و آموزش آمار دارید با ما در میان بگزارید.
به عنوان مثال: نمودار سبک مورد علاقهی افراد در فیلم
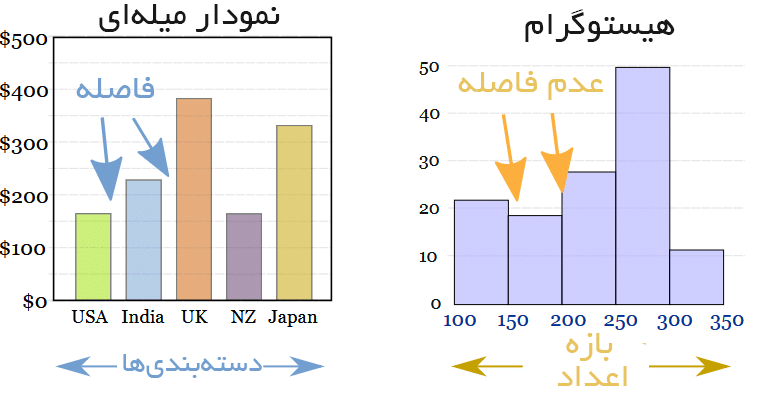
مقایسهی نمودار میلهای با بافت نگاشت:
نمودار دایرهای(circle chart) یا (pie chart) :
نمودار دایره ای در علم آمار و آموزش آمار یک نمودار ویژه است که از قطاعهای دایرهای برای نشان دادن اندازه نسبی دادهها استفاده میکند. ساده ترین تمثیل برای نمودار دایرهای، تشبیه آن به یک پیتزا است. بدین ترتیب میتوانید قاچهای پیتزا را قطاعهای نمودار در نظر بگیرید
محاسبه شاخص های مرکزی:
در محاسبات آماری لازم است که ویژگیها و موقعیت کلی دادهها تعیین شود.برای این منظور شاخصهای مرکزی محاسبه میشوند.
شاخصهای مرکزی در سه نوع نما (mode) و میانه (median) و میانگین (mean) هستند.
وقتی از شاخصهای گرایش به مرکز مانند میانگین صحبت میکنیم یعنی میخواهیم یک نماینده از دادهها را به جای کل مجموعه دادهها ارائه میدهیم.
- میانگین نمایندهای از داده هاست که اگر به جای تک تک داده ها آن را ارایه دهیم در مجموع ارائه شده تغیری ایجاد نمیکند.
به عنوان مثال سه عدد 2 و 3 و 4 را داریم .مجموع این اعداد 9 است. حال میخواهیم به جای این سه عدد یک عدد قرار دهیم که مجموع داده ها حفظ شود ، تنها عددی که این ویژگی را دارد میانگین این اعداد یعنی عدد 3 است.
برای محاسبهی میانگین مقدار تمام دادهها را جمع کرده و بر تعداد آنها تقسیم میکنیم.
همینطور که از فرمول مشخص است ، میانگین فقط برای دادههای کمی مناسب است و محاسبه برای دادههای کیفی کاری غیر منطقی است.
یکی از معایب میانگین این است که تحت تاثیر دادههای پرت قرار میگیرد .مثلا میانگین اعداد 1000 و 8 و 6 و 4 و 2 عدد 204 است که نمایندهی خوبی برای دادهها نیست .
پس در ارائه تجزیه و تحلیل و گزارشهای آماری ، بیان یکی از شاخصهای مرکزی به تنهایی کافی نیست.
نماد (mode) در آمار:
مشخص کنندهی داده ایست که بیشترین فراوانی را دارد .
همانطور که از تعریف مشخص است در نما نوع داده اهمیت ندارد بنابراین هم برای دادههای کیفی و هم برای کمی مناسب است .
مثال: نما یا مد را در دادههای زیر بنویسید.
با توجه به تعریف نما داده ایست که از همهی دادهها بیشتر ظاهر شود با توجه به اینکه عدد 4 ، سه بار ظاهر شده بنابراین 4 نما ، است.
میانه (median) در درس آمار:
برای متغیرهایی که مرتب کردن آنها از کوچک به بزرگ امکان پذیر است ، میتوان میانه محاسبه کرد.
برای بدست آوردن میانه ابتدا دادهها را از کوچک به بزرگ مرتب میکنیم دادهای که در مرکز قرار میگیرد را میانه گوییم.
میانه شاخصی است که 50 درصد دادهها از آن کوچکتر و 50 درصد دادهها از آن بزرگترند.
اگر میانه و میانگین یکی باشند، توزیع مقادیر کاملا متقارن خواهد بود.
چارکها در علم آمار و آموزش آمار چیست؟
در آمار چارک ها نماینده هایی هستند که برای نشان دادن وضعیت و ارائه اطلاعات خلاصه در رابطه با یک مجموعه داده، ارائه می شوند.
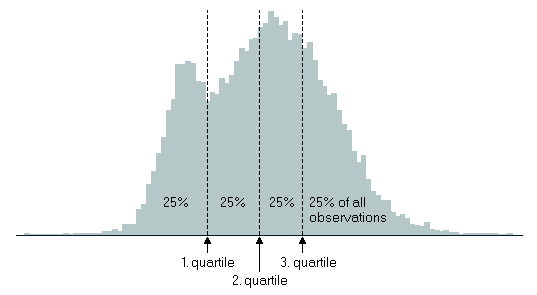
چارک اول
مشاهده ای از مجموعه داده های مورد بررسی است که یک چهارم داده ها (یعنی ۲۵ درصد مشاهدات) از آن کوچکتر و سه چهارم داده ها (یعنی ۷۵ درصد مشاهدات) از آن بزرگتر می باشد.
ابتدا میانه داده ها را بدست آورده سپس برای نیمه اول داده ها (از کوچکترین عدد تا میانه) مجددا یکبار دیگر میانه را محاسبه می نماییم.
این عدد که میانه نیمه اول داده ها است همان چارک اول می باشد.
چارک دوم
چارک دوم همان میانه می باشد، داده ای که ۵۰ درصد (نیمی) از مشاهدات از آن کوچکتر یا مساوی و ۵۰ درصد (نصف دیگر) از آن بزرگتر می باشند.
چارک سوم
مشاهده ای از مجموعه داده های مورد بررسی است که سه چهارم داده ها (یعنی ۷۵ درصد مشاهدات) از آن کوچکتر و یک چهارم داده ها (یعنی ۲۵ درصد مشاهدات) از آن بزرگتر می باشد.
ابتدا میانه داده ها را بدست آورده سپس برای نیمه دوم داده ها (از میانه تا بزرگترین عدد) مجددا یکبار دیگر میانه را محاسبه می نماییم.
این عدد که میانه نیمه دوم داده ها است همان چارک سوم می باشد.
چارک چهارم
چارک چهارم مشاهده ای از مجموعه داده های مورد بررسی است که کل مشاهدات (یعنی ۱۰۰ درصد داده ها) از آن کوچکتر یا مساوی می باشند.
در واقع چارک چهارم همان ماکزیمم یا آخرین عدد در ترتیب مرتب شده داده ها از کوچک به بزرگ می باشد.
اگر در رابطه با این مقاله اشکال و ابهامی دارید می توان در قسمت کامنت ها بیان نمایید تا ارائه توضیحات اضافه ابهام شما برطرف شده و موضوع شفاف تر گردد.
همچنین در صورتی که در رابطه با موضوع این مقاله تمرین و یا سوالی دارید که پاسخ آن را نمی دانید، می توانید در قسمت کامنت ها سوال خود را بیان نمایید تا بررسی و پاسخ داده شود.
شاخصمرکزی به تنهایی شاخص خوبی نمیباشد و باید شاخص دیگری که میزان پراکندگی داده ها را مشخص میکند نیز بررسی کنیم.
شاخصهای مرکزی به تنهایی قادر به مشخص کردن توزیع دادهها نیستند و از شاخصهای پراکندگی باید برای تعیین میزان گستردگی مشاهدات استفاده نمود.
شاخص های پراکندگی متعددی وجود دارد که در ادامه آنها را بررسی میکنیم.
دامنه تغییرات ( range) :
سادهترین شاخص پراکندگی است و برابر است با تفاضل بزرگترین و کوچکترین داده .
ایراد این شاخص این است که تنها به بزرگترین و کوچکترین داده توجه کرده و چگونگی قرار گرفتن دادهها بین این دو مقدار را در نظر نمیگیرد.
ایراد دیگر این شاخص این است که اگر دادهها شامل دادهای پرت باشند، دامنه به شدت تحت تاثیر آن داده قرار میگیرد.
واریانس(variance ) :
پرکاربردترین شاخص پراکندگی است.
برای محاسبه واریانس باید به صورت زیر عمل کنید:
- ابتدا میانگین را حساب کنید.
- سپس مقدار میانگین را از هر یک از دادهها کم کنید و نتیجه را به توان دو برسانید .(مربع اختلاف)
- در نهایت میانگین مربع اختلافات بدست آمده را بدست آورید.
اگر واریانس صفر باشد ، تمامی دادهها(مشاهدات) برابرند.
هرچه واریانس بزرگتر باشد ، مقدار پراکندگی مشاهدات بیشتر است .
انحراف معیار(Standard deviation) :
یکی دیگر از شاخص های پراکندگی است که همانطور که مشاهده میکنید از دو واژهی انحراف و معیار تشکیل شدهاست ، انحراف به معنای میزان دوری هر عضو یک مجموعه داده از میانگین و واژهی معیار به معنای استاندارد بودن آن است .
هرچه انحراف مجموعهای از داده ها عدد پایین تری باشد ، نشانگر آن است که دادهها به میانگین نزدیک تر هستند و پراکندگی اندک است و در صورتی که انحراف معیار عددی بزرگ باشد، نشان میدهد که پراکندگی دادهها زیاد است.
ضریب تغییرات (Coefficient of Variation):
یکی دیگر از شاخصهای آمار توصیفی که اغلب برای نمایش و مقایسه میزان پراکندگی بین دو جامعه یا دو متغیر به کار میرود.
ضریب تغییرات برابر است با تقسیم انحراف معیار بر میانگین.
از آنجایی که کم بودن پراکندگی، نشانگر همگن بودن جامعه است، هر چه میزان ضریب تغییرات کمتر باشد، میانگین را معیار بهتری برای نقطه تمرکز مییابیم. بنابراین در بین دو جامعه، آن که دارای ضریب تغییرات کمتری باشد، جامعه بهتری بوده، زیرا نتایج گرفته شده از شاخص میانگین، دقت بیشتری دارند.
بدلیل اینکه ضریب تغییرات بوسیله یک نسبت از کمیتهای هم واحد، محاسبه و ساخته میشود، هیچ واحد اندازهگیری نداشته و به صورت درصدی مورد استفاده قرار میگیرد. همین موضوع نیز اهمیت استفاده از این شاخص را برای مقایسه بین جوامع مختلف، مشخص میکند.
فرمول های محاسباتی علم آمار:
ما در این جدول برای شما تمامی فرمول های محاسباتی علم آمار و آموزش آمار را برای شما قرار دادیم.
امیدواریم این جدول به شما کمک کند.
اگر هم سوالی در رابطه با فرمول های محاسباتی علم آمار از ما بپرسید.

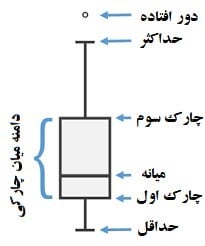
بعد از آشنایی با معیارهای پراکندگی قصد داریم با استفاده از نمودار جعبهای ، معیارهای پراکندگی و مرکزی دادهها را به صورت تصویری نمایش دهیم.
در این نمودار چارک اول ، میانه ، چارک سوم ، بیشترین و کمترین مقدار دادهها به صورت همزمان نمایش داده میشوند.

این بود چکیدهای از علم آمار و معیار های مرکزی و پراکندگی، اگر این مقاله مورد توجه شما قرار گرفته است ، به لینک زیر هم سری بزنید






